Toy Philosophy Universes (part 2)

In the first installment on toy philosophy universes, I gave a rudimentary account of one of the main motivations behind this series: the problem of stepping outside of the model or the system an agent inhabits or broadly speaking, the metatheory of theorization.

To be candid about it, I do not think that philosophy or for that matter natural sciences, mathematics, logic or even theoretical computer science are, by themselves, capable of offering an adequate solution to this problem which for now can be dubbed as the transcendental jailbreak (in reference to Wittgenstein’s Prison and my previous comments on the Kantian straightjacket).

If there is a solution to this problem, it is in a non-trivial integration of all the above fields of thought. Non-trivial in that none of these fields can be subordinated to or assimilated by one another. That is to say, for philosophers attempting to tackle this problem there is no other option other than integrating and rendering contemporary the discipline of philosophical inquiry with sciences (complexity sciences in particular), mathematics, logic and computer science. Indubitably, through the course of this upgrade and revision, the very nature of philosophy as a discipline will transform: We begin to see the phantom-like apparitions of what from the perspective of here and now might have only some vague and negligible resemblances with what we currently characterize as philosophy.

The future philosophy—even as a Platonic eidos—cannot be anything but a program for thinking globally about thinking about the world, migrating—step by step—from the conceptual system which undergird our local conception of the world to a metalogic of such conception, adopting a view that no longer bottoms out in our particular (multi)perspectival view of the world.

Now allow me to return to what I characterized in the previous post as a chronic cognitive voyeurism, that is, a child-like fascination with the implicit know-hows and know-thats behind our attempts at forming a theory, model or conception of this or that aspect of the world. What are the questions I ask myself when confronted with a theorist’s output? Some of the immediate question are ‘What kind of implicit system of search and assembly do they use when they work, what does their toolbox of methods contain, what reasoning or cognitive mechanisms (analogical, deductive, etc.) are being activated, and more importantly, can all of this be modeled, can it be replicated or implemented in another context? What I wish to know are not only the very mundane habits of thinking, writing, note gathering, etc. but also and above all, the metalogic of one’s logic of theorization or more generally the implicit thoughts which go into one’s explicit thinking about the world…and ultimately, how all of these things fit together, how much—if at all—and at what level do they influence one another.

Yet this exploration of the metalogic of one’s logic of the world is anything but a straightforward affair. It requires an understanding of not only how we model the world but also what it takes to go beyond that model while suspending the model-biases and more importantly, the dogmas of our particular transcendental type or perspectival (or intuitive in a Kantian sense) resources. With these cursory remarks let us begin this series:

0. Welcome Back to Kindergarten

Are you sick of philosophical -isms? Do you believe that there are so many rival and incompatible philosophical views that they almost inevitably will lead you toward feud-ridden tribalism? Are you tired of being a professional philosopher? Do you feel as if the discipline of philosophy as it stands today has betrayed our initial ambitions and excitements? We signed up for expansive cognitive exploration, but instead we ended up in pigeonholed tunnel-visioned analyses or worse, some all-over-the-place theses which purport to be impersonal but are in fact fanatically personal and simplistically psychological through and through? We either succumb to the monism of methods and models or its pluralistic twin which is in reality a relativistic soup with little to zero consistency. Do you often dream of being once again a child-philosopher rather than a jaded adult scholar? Do you approach your models or conceptions of the world as toys which can be discarded or broken in the real world but not until they are sufficiently played with or do you see them as mature completed narratives? As a philosopher or theorist, which one is the universe you live in, a toy philosophy universe where endless constructibility, experimentation and rearrangement of multiple models are the norm or an elegant fully-completed house where you as an adult have finally settled? Lastly, do you think that the pedagogy of the philosophical discipline is responsible for how we think about the world. If the answer is positive, then given the current philosophical pathologies, how should we reconcile the discipline of philosophy with its education?

The bad news is that—and there is always only bad news—this series attempts to tackle these concerns with questionable or no success. But we as philosophers and theorists are in the business of epistemological risk and theoretical humiliation. We neither take the failure of a hypothesis as a negative outcome or an irrefutable evidence that the failed hypothesis will invariably fail in every context, nor do we conflate the unreachability of long term objectives from our today’s perspective as a good argument against our attempts to systematically and concretely entertain such objectives. To this extent, in this and future installments, I precisely tackle with such questions. The aim is to elaborate the concept of toy philosophy universes as a partial answer to the above questions.

For now, this elementary definition should suffice:

However, to methodologically reach this definition through which we can finally in a coherent manner tackle the aforementioned questions, we must first engage with a whole slew of related questions: What are toys? What are models? What does the contemporary science of modeling involve? How can the praxis of philosophy be informed by the science of modeling? What are toy models? In what respects big toy models differ from small ones? Is there a set of canonical formalization for such models for the purpose of exact reconstruction and reimplemtation within a context that is not predominantly scientific? How can we see both theoretical and metatheoretical assumptions as necessary to the labor of modeling? What does exactly differentiate toy philosophy universes from big toy models? What are the implications and outcomes of living in a toy philosophy universe as opposed to a purely scientific one?

In a nutshell, we cannot investigate what it means to step outside of our theoretical models unless we first examine what modeling, theorization and metatheorization entail. Given the above list of questions, it should be clear by now that the path this series takes is going to be circuitous and hazy. The first few posts will be introductory and light, but as we move forward indulgence in technicality and formalism will become inevitable.

I will engage, first of all, with toys, elaborating on the idea of ‘toying around with our models of the world’ using examples derived from the history of pedagogy and engineering. Next, I shall focus on the science of modeling, the principles behind how we scientifically model an aspect of the world. Subsequently, I will move to the domain of toy models and so on.

We all remember a moment in our childhood when toys were our surrogate parents, far more generous, interactive, manipulable, cooperative and informative than our parents. Perhaps, toys first—and not the preachings of our adult guardians—made us realize that there is a world out there, a world that despite its malleability is constrained by what we eventually learned is called objectivity. Recall those nights when we chose the company of toys over adults, we chose to sleep in a tent made of a few pillows simulating the environment of a universe brimmed with possibilities. There was a mountain outside—a cardboard box covered with a brown satin. The meadow inside the tent was comforting and smelling nice. But it was an an old smelly green blanket shrunken and wrinkled after being washed in hot water for many times. In that very tent, we waged war against three metal pencil sharpeners which looked like three thousand armored cavalry units. We were at the end triumphant. The three colored pencils staved off the advance of the metal sharpeners after much sacrifice. They are now far shorter than what they once were. The remaining forces are currently in an eternal alliance. They are the people of this tent which I call my world. After we concluded the battle, we fell asleep dreaming of a bigger tent with ever more new alliances, new friends. But the peace did not last long, for soon a flying saucer carrying an army of disfigured teaspoons delivered a cryptic message, ‘there is a world out there even larger than your toy universe’.

Among the greatest educationists, from Friedrich Fröbel to Rudolf Steiner, Leo Tolstoy, Jean Piaget and Lev Vygotsky, the idea of toying around with the furnitures of the world has been advanced as one of the most important aspects of education, that is, the augmentation of autonomy (what I am and what I can do in the objective world). Philosophy of toys in a sense takes seriously the idea that education does not end with autonomy or with the initiation into the space of theoretical and practical cognitions. On the contrary, it sees the autonomy of the child, the child’s synthetic ways of manipulating and understanding things, its proto-theoretic attempts at constructing a world prior to even conceptualizing that world as the premises of education. For this educationist philosophy, the role of toys in the recognition of the child’s autonomy and world-structuring abilities are more than necessary. They are indispensable.

1. From Logos to Lego and Back

We can only represent the world to the extent that we have built a world in which our representations coherently hang together. The scope of our world-buildings demarcates the limitation of our attempts at representing the world. Take for instance, Carnap’s Versuch einer Metalogik (Attempt at Metalogic) or The Logical Syntax of Language after the failure of his logical empiricism program in Aufbau or more recently, the work of Uwe Petersen. Despite their methodological and objective differences, in both cases we see that the frontiers of objectivity or what we call the object or object-constitution (or alternatively, Being, the intelligible, etc.) are set by the scope of our attempts at the construction of what we call theory or more precisely, in the case of both Carnap and Petersen, by the logical structure (albeit in each case the question of the logical structure is formulated differently). This line of thought is, of course, guaranteed to elicit the ire of orthodox Kantians who may still believe in the hard distinction between form and content or opposing logic as a canon to logic as an organon which according to Kant is the logic of illusion or a sophistical art (CPR, B86) on the grounds that it is not constrained by the empirical sources of truth, sensible intuitions or information outside of logic.

What Kant means by logic as an organon is roughly a formal tool for the production of objective insights or an instruction for bringing about a certain cognition that can be said to be objective. This conception of logic is then characterized as the science of speculative understanding or the speculative use of reason—the organon of sciences (CPR, A16-18). On the other hand, logic as a canon refers again to the formal use of logic (regardless of it content which can be empirical or transcendental) but this time as restricted to the characterization of logic as the canon of judging (i.e. the mere criteria of the correct application of the laws of thought or judgements) which requires and is constrained by extra-logical information (CPR, A61).

At this point, I do not want to discuss in details the fact that Kant’s opposition of logic as a canon to logic as an organon is a historical take on the controversy between Epicurus (the defender of canon) and Aristotle (the defender of organon). Or the fact that Kant’s dismissal of logic as an organon is entirely based on an antiquated Aristotelian definition of logic. Regardless, of how we interpret logic, this very distinction becomes manifestly precarious in the wake of revolutions in formal and mathematical logic in the twentieth century. With the advent of computation as the proto-foundation of logic—thanks to the so-called Curry-Howard-Labmek correspondence—the last residues of the Kantian contrast between logic as a canon and an organon fade away.

Even though we will return to the above issue to examine it closely, for now, we can always counter the objection of orthodox Kantians with a brief retort: So you think that form without content is arbitrary (i.e. unconstrained), but could you tell me what is a content without form? Surely, entertaining the possibility of the latter even under the most watchful eyes is another variation of that ideological house of cards which is called the Given. The whole notion of logic as a canon describes a game of logic already rigged by the representational resources and limits of the apperceptive subject constituted within a particular transcendental type.

In contrast to Uwe Petersen’s rebuke against Kant in the second volume of Diagonal Method and Dialectical Logic, I think Kant’s distinction between canon and organon, logic as world-building and logic as constrained by world-representation is quite subtle. Yet subtlety is not by itself a criterion of truth or profundity. For Kant seems to naively assume that thinking about logic as an organon means believing that we can ‘judge of objects and to assert anything about them merely with logic without having drawn on antecedently well-founded information about them from outside of logic.’ (CPR, B85, my emphasis).

What is important to recognize in the above quote and other passages concerning logic in CPR is the constant repetition of such focusing adverbs as ‘merely’, ‘solely’, etc. Kant seems to be peddling a trivial and obvious point not only as a profound remark but also as a refutation of the conception of logic as an organon. Yes, at least since the time of Plato’s Sophist, we know that what is said is not equal to what is. And indeed, the equation of the two is the core tenet of sophism: As long as I know the rules of deductive syllogism I can call myself the master of all sciences. But logic as an organon neither implies the aforementioned equivocation—i.e. the claim that logic is by itself sufficient for judging about the stuff in the world—nor requires any metaphysical commitment with regard to logic—i.e. the claim that laws of thought are laws of the world.

In contrast to Kant’s straw-manning of organon, all the conception of logic as an organon suggests is that our resources of world-representation are in fact beholden to and caught up within the scope of our world-construction, and in this case, the world of logics. In other words, it would be absurd to even talk about objects without the primacy of logical structure or logoi. Kant would have agreed to this sentiment but only in a trite manner. Why? Because if the talk of object is meaningless without theory or logical structure, then the expansion of the field of logic or determinate thought-forms unconstrained by all concerns about representation would be an absolutely necessary step to constitute objects, make objective assertions and deepening our discourse about objectivity. This primarily unconstrained view of logic as the indelible factor for object-constitution is exactly what we can call logic as an organon. Without it, all we can ever achieve are pseudo-talks of stuff i.e. Aristotelian this-suches or tode ties, namely, unstructured encounters with items or stuff in the world which have no objective structure or invariant qualities.

Moving from the sense impression fuzzy mass of cubic redish (materiate individual substance or stuff) to this red Lego block (a perceptual taking or judgement) requires the addition of logical structure. But the constructive characterization of logical structure is not a priori limited by representational concerns. Indeed, to adequately hone out the notion of logical structure demands the treatment of logic and logical world-construction in terms of general logic in itself, that is to say, unconstrained by any enforced representational consideration (whether the experiential content, the empirical source of truth or the the criteria of correct application of logical laws to items of the real world) that may establish the frontiers of logic in advance.

It is only when we attempt to decouple logic from any representational or world-referring constraints that we can ensure a sufficiently enrichable framework of world-representation. In short, to expand the resources of representation and enhance the correct application of logical laws to empirical evidence or observational statements, we must first engage with logic in its own terms and expand its domain not in accordance with but in spite of representational constrains. The world-constructing resources of logic in itself precede and in fact undergird the world-representation, our understanding or judgements about the world. To make a Carnapian slogan, construction of the world is prior to the constitution of the object and the knowledge of it. This priority is not only priority₁ in the sense of one temporally preceding the other, but also priority₂ in the order of constitution. It is priority₂ which is, properly speaking, the focus of logical world-construction and describes the conception of logic as an organon.

How can we constitute an object or even entertain the idea of objectivity in any coherent manner if we do not take seriously the world-construction of logic (i.e. the organon) so as to broaden the domain of logic within which the object coheres and the notion of objectivity is deepened? If we choose to abandon this path in favor of the Kantian conception of logic as a canon, then we are eternally sentenced to what I have called the Kantian straightjacket i.e. those particular transcendental structures we inhabit and by virtue of which we will never know whether our objective descriptions of the world are the overextetions of our specific (sensible) intuitive resources or not.

Taking the idea of logic as a world that ought to be infinitely constructed without any prior restriction is in every sense incommensurable with the idea of logic as something that ought to be coordinated with the real world in the first instance. Kant’s transcendental logic as a species of pure specialized—i.e. concerned with particular use of understanding—logic is precisely a conception of logic that is not just conservative with regard to the possible scope of logic (how general logic can be expanded and enriched) but also insofar as it is built on the conception of logic as a canon—i.e. constrained by representational concerns—it harbors epistemic implications which are nightmarish to the say the least.

With reference to the previous installment, this epistemological nightmare or hell is more than anything the consequence of our own self-imposed restrictions and not simply, the result of our local and contingent constitution as such and such subjects (history of evolution, the structure of memory, culture, etc.) When we limit logic to representational considerations while our representational systems are at the bottom rooted in a particular transcendental type which delimit our empirical observation and often distort our objective descriptions, then the epistemic or objective imports of our logical systems only reiterate or overextend the limitative terms of our representational biases. The picture of the objective world we provide resembles the portrait of Dorian Gray: only more sinisterly subtle variations of ourselves and our entrenched dogmas, and nothing more.

The only viable strategy for gradually escaping from this Dorian Grayesque ordeal is to take seriously the priority₂ of world-construction over world-representation and to avoid subordinating the treatment of logic to any extra-logical concern that might have the faintest smell of representation, empirical point of reference, ordinary conception of meaning or anything that sets the boundaries of logic in advance.

The great escape only begins when logical construction is separated from the province of the apperceptive subject and its ordinary affairs. It is no exaggeration that the unbound realm of logical construction is analogous to an infinite ocean within which islands of subjectivity or apperception emerge and disappear. And in fact, this analogy is becoming more and more the very shape of the future logos: What I have called general artificial languages already offer us the inklings of that slippery yet boundless divine notion which we call logos and whose personifications are logic, mathematics and computation. Within this artificial apeiron—artificial language as the lego of future reason—our natural languages are but destined to corrode and eventually sink akin to tiny islands whose once firm ground can no longer withstand the rise of sea-level.

Made possible by the conception of logic as an organon, this apeiron is nothing but the universe or universes of metalogics or metalanguages. In other words, the logical apeiron does not signify one universal language or metalanguage, nor does it represent a final stage in the construction of language as the interface with reality or the configuring factor of the objective world. By contrast—and with a nod to Carnap in Logical Syntax of Language—no single language even in the most generic sense (i.e. not a natural language) can exhaust the logico-computational structure of language. For delving into the structure of language requires ever more richer languages or an infinite nested space of metalanguages or metalogics (a la Gödel).

It is in this respect that the plural designation general artificial languages simply describes what is already the case with logic and mathematics: No single system or language is adequate to explore the structure of language, logic or mathematics. Only an infinitely constructible—that is to say, not limited in advance in the vein of logic as a canon—nested space of metalanguages. Even the mighty Sellars treat the space of metalanguage as an applied domain and a completed totality by which we can resolutely talk about the structure of natural languages and such thing as semantic value and syntax. Contra Sellars, the space of metalanguage is not like an orthodox vantage point from which we can conclude the structure of meanings as assertions or finalize the definition of meaning as classification. Put differently, metalanguage as a nested constructible apeiron cannot even be compared to something like a completed vantage point for comparing two natural languages in order to decide the classificatory role of meaning (e.g., •red• in english means •rot• in german i.e. red plays the same classificatory role that rot plays in German). The whole point of metalanguage is the exploration of the very conditions of possibility of meaning as classification and structure, rather than as a light comparative study between this or that established language. Sadly, there are only a handful of philosophers and logicians for whom the domain of meta- is likened to an infinite heaven—an infinite nested space that is not arrested by the criteria of world-representation but unbound by the possibilities of world-construction in the domain of language and logic as organons.

The world-building of language just like logic mirrors the metaphor of ascending to metalinguistic heavens or descending into the abyss of metalogics depending on one’s theoretical proclivities and aesthetic sensibilities. In either case, what is crucial is the understanding that what is constructible by definition is never arrested by limits drawn in advance. Forgoing this notion of established boundaries for language and logic demands a concrete commitment to logic as an organon rather than a canon, to approach world-building as prior₂ to world-representation.

2. Who wants some Fröbelian gifts, raise your hand!

With this digression on world-construction versus world-representation, toys versus adult concerns about the knowledge of the real world, let us return to the territory of actual toys.

The kindergarten philosopher, the child, is absorbed in that immense universe which is that of world-construction. The child’s toy universe does not resemble anything like the represented world of ours. The toy blocks by which the child assiduously constructs a world are not anything like bricks cemented over bricks. They can be replaced or even discarded if the child is not satisfied with the result. And we all know that a child never gives up. Until the toy-made world is in its optimal condition, it will be destroyed again and again. Even when the optimal construct is achieved, nothing guarantees that the child won’t reengineer it the next day to accommodate more adventurous narratives. This is the very definition of infant politics from which we adults have regrettably diverged.

The interaction of the child with toys is a premise upon which the objective interaction of concept-using adults and the world is built. The philosophy of toys in this respect precedes the philosophy of education qua augmentation of subjective autonomy i.e. what I can do and say in the objective world. What distinguishes toy-education from the canonical formula of graduation to adulthood—coinciding with full-blown conceptual competency—is that toys are not just about language but also the use of tools. They are as Vygotsky suggests the zones of synergy between language-use and tool-use, acquaintance with world-representing resources and world-making or world-reengineering techniques and systems.

A child who is immersed in playing with toys is a symbol-tool explorer. The child sees language as a tool just as it sees tools as symbolic-combinatorial elements of the language. The boundary between building the world and representing it is blurred and sometimes non-existent. It is in this sense that comparing the role of toys for a child to something like tools might be very well a symptom of our rooted adult misunderstanding. It is only, analogically speaking, from our adult perspective that we can remotely compare toys with tools. But toys, adequately understood, are not tools per se. In contrast to the use of tools, toys do not strictly adhere to pieces of practical reasoning (e.g., In order to achieve X, I ought to do Y). The ends of toy-plays are not like the ends of our practical reasons which go away once we attain them. They are more like inexhaustible ends, or ends which do not simply go away once achieved. For as long as, the world can be reconstructed and re-engineered, the infinite prospect of the kingdom of ends is at hand.

However, toys as I mentioned earlier are not just the blocks of world-construction. It is well-established (e.g., Spatial Reasonin in the Early Years) that toys play an essential role in the world-structuring capacities of children. The augmentation of spatial reasoning and correspondingly, the later use of mathematical concepts such as complex transformations, mapping, transfer, symmetry, inversion, shearing (in the case of paper-toys) and so on are directly linked to how children play with toys.

Block-oriented toys such as Lego introduce children to extremely potent and specialized concepts like modularity. It would be hard—if not impossible—to imagine the scope of technological progress and above that, the discipline of engineering as a tissue connecting the messy problems of physics with mathematics without the concept of modularity. Even though modularity is an epistemic concept rather an ontic one, I am yet to be convinced by the arguments of those philosophers who think certain structures in the universe, for example brain, cannot be modeled modularly. The majority of such critiques assume that modularity means something similar to Khrushchyovka-like buildings where modules are put atop one another to create something that is too rigid and monolithic to afford anything resembling organic life. But modularity comes in varieties of forms. Every complex can in one way or another—after sufficient approximations—be modeled via the surprising efficacy and flexibility of modular systems. It is true that modular models distort some information concerning target systems, but then which models are exactly distortion-free? The modeling-epistemic war against modularity is more than anything a product of unwarranted metaphysical assumptions about the structure of the universe and the inadequate grasp of the concept of modularity than anything else. See for example the recent works of Andrée Ehresmann, Jaime Gómez-Ramirez and Michael Healy who have synthesized the insights garnered from category theory and algebraic geometry with those from brain sciences.

Speaking about the territory of toys as tools for the enhancement of world-structuring abilities or faculties would be impossible without at least a brief reference to Fröbel’s original notion of kindergarten and Steiner’s school of Waldorf education. Think of Fröbel’s gifts, multiple sets of toys starting with regular wooden blocks. Once a child masters the use of a toy-set or a Fröbel gift, it is awarded a new set of toys, for example, geometrically disparate wooden blocks plus colored strings. The point of the toy gift-giving is to raise a child with the understanding that world-construction is an infinite domain. The further you attempt, the more world-building components fall from the sky. If you think you have achieved a perfect world, then let me give you a new set of constructive units, namely, toys.

The same thing holds for Steiner’s school of Waldorf education. Think of a Waldorf doll, a faceless uncharacteristic doll made of the cheapest material and stuffed with hay. The child begins to learn that the doll is not the true object, which is to say, the object is always incomplete. The child then goes on to paste a smily face, a big nose and dark brown eyes which it had drawn on a paper on the doll’s face. However, depending on the setup of the child’s toy universe, the doll can take fundamentally new characteristics like a platform on which new qualitative differences can be built, layer after layer.

From our adult perspective, there is hardly anything more grotesque than a Waldorf doll laying around, one with which a child has played for months. But as if beauty in the eye of a child could be anything other than something in essence synthetic, layered and transitory: faces pasted on faces, vestige upon vestige, characters built on top of one another all within one domain, the toy universe. Within this universe which is a featureless doll, the original beginning and the ideal end are never attainable, only residuation of what has come before and the possibilities of further construction.

Similar to Waldorf dolls, the main emphasis of Fröbel gifts is also world-building. Although the gifts shift their focus to a more systematically disciplined mode of construction and less the free-play of simulating or imaginative capacities. Climbing the hierarchy of Fröbel gifts demands new forms of spatial reasoning, geometrical pattern matching and bootstrapping techniques, and sophisticated intuitions into the realm of naive physics. As the level of the gift goes up, the child’s construct becomes increasingly similar to a genuine marvel of modernist architecture or an experimentally engineered contraption straight out of the Rube Goldberg-inspired videogame, Crazy Machines. Nevertheless, in both cases, we see a coupling between world-building and simulational abilities. The point of toys is as much about world-construction as it is about building up the capacities and techniques of simulation through which understanding is amplified and its scope is expanded.

We already know from Kant that what we call today simulation in a loose sense—as in simulating a world in which friction does not exist—is at the bottom the function of productive imagination which in the Kantian parlance is just understanding in a different guise. Behind productive imagination lies one of the key themes of Kantian transcendental method: the argument about schemata. Schematism addresses one of the most weighty problems in transcendental philosophy, the so-called homogeneity problem i.e. the correspondence or coordination between concepts qua rules and objects or imagistic impression of items in the world. By image, Kant means a singular rudimentary (i.e. intuited) representation of an item / object. One can think of the rudimentary imaging faculty as involving extraction and integration of salient perspectival or local features qua variations of an object. Concepts on the other hand are non-perspectival (the invariant). They are at the most basic level principles of unity through which multiple particular instances can be brought predicatively under one subject, particularly a logical subject. Once we have concepts, we can arrive at critical perceptual judgements so that when we look at a Bic pen immersed in a glass of water, we can assert that this such-and-such pen looks—perspectivally—bent but is in fact straight. This is a piece of critical perceptual judgement or taking i.e. grasping, understanding or conceiving (bringing into conception). In contemporary terms, then we can think of the homogeneity problem as the problem of coordinating local variations and global invariance (the core of sheaf logic) or particularities and universality, eikones and ideai, the temporal capacity aisthesis and the time-insensitive faculty nous (the problem of Plato’s divided line). Let me clarify the homogeneity problem with an analogy to Euclid’s Elements.

Think of this particular equilateral triangle, this particular isosceles triangle and so on. These triangles are just particular—i.e. locally-varied—shapes or image-models. In reference to Proclus’s commentary on Euclid, they are only triangles by virtue of falling under the concept of triangularity as such. The triangle as a concept then allows us to make certain kinds of judgements or to draw diagrammatic inferences (Euclidean demonstrations) with regard to any triangle in whatever possible configuration.

Now the homogeneity problem engages with the issue of how can this or that particular triangle can be coordinated with triangularity as such. Put differently, how can the concept be supplied with its image. Proclus thinks the solution is in what he calls a mediating universal, a rule that comes between the detached universal (the universal triangularity inexhaustible by any image of a triangle) and particular triangles. Kant calls these mediating rules, schemata. Schematism then describes rules or constructive procedures which unlike the strong sense of the concept are not concerned with what particular image is subsumed by a concept, but how a particular image can be constructed in thus-and-so ways so that it conforms with a certain concept. This howness designates the functional role of the concept qua rule. Functional in the sense that we use the concept of triangularity whenever a particular item—an imagistic shape of a triangle—is implicated in the actual use of the concept of triangularity.

A schema is then simply the representation of a general procedure or rule of imagination (i.e. the capacity to represent an object even without its presence in intuition) for providing a concept with its image. But what kind of image and what kind of rule? The answer is a perspectively determinate sensible image which connects the single concept and the varied images. In Euclidean terms, we can think of a schema as triangularity not as a detached universal eidos, but as a formula for how to configure and diagram such-and-such lines, angles and vertices. For example, according to Proclus, just as there are mediating universals or rules which supply the concept of triangularity with triangles which might be equilateral, isosceles, etc, there are also construction rules or recipes of configuration (mediating particulars) which enable us to construct triangles using lines and angles as their elementary blocks for particular types of triangles (the concepts of scalene, isosceles, and so on).

Essentially, the schema as the missing link between understanding and sensibility, has one foot in categories (pure classificatory concepts) and the other in the intuited object or the image qua appearance. Thus we can say that a sensory presentation and a singular conceptual representation are determined by one and the same schema, that is to say, one and the same concept of a determinate mode of sensory presentation through which the concept and the object or its imagistic presentation come together. A schema is in this sense not a rule as that which predicates but as a recipe for construction of locally varied images for a single concept.

When it comes to schematism, Kant is actually quite fond of non-empirical examples like drawing a straight line in thought. A recipe or rule for drawing a straight line is at once responsive to two criteria: (1) every segment that is built is drawn in relation to the concept of line as a whole or that which binds all segments together, and (2) every piece or segment is constructed on the segment that has come before it (the law of memory which in Kant’s work can be attributed—with some reservations—to inner sense). With regard to both #1 and #2, we can say that the ultimate coordination between the image and the concept happens in the realm of rules (of construction) as pertaining to how such and such phenomenal features are being organized or brought together by space and time as transcendental idealities.

Therefore, as long as we are endowed with different spatio-temporal principles of organization, we can imagine of schemata which bind the imagistic item and the concept in different ways. Lucky for us, a child who is still in the process of coming to grasp with representations of time and space can vary the very parameters by which the image is related to the concept. This is what I call infantile schematism and by that I mean a child never settles for a particular established image for a concept. This is but the very law of simulation.

You say that the concept of mountain should conform to such putative invariant image-models. ‘Daddy I do love you but you also happen to be so parochial,’ the child opines: ‘Let me set you straight, in my toy universe, the mountain can be anything. It can be a cardboard box covered with brown satin or it can be a pot of old coffee’. The child then continues, ‘you think just because I play with what I call humans, they should conform to what you perceive as a human. But you are sadly mistaken for even a colored pencil wearing a thimble can be a human, an autonomous agent in my world.’ This is what simulation is all about. It does not matter what imagistic impression of an item in the world corresponds to a concept. What matters is the mediating rule of how any imagistic impression—after the sufficient relaxation of representational constraints—can be coordinated with a concept which is applied across the board for all instances brought under it.

Accordingly, simulation in the aforementioned sense involves destabilization of a canonical or stable set of images for a concept. But this process of destabilization is followed by a process of restabilization so that the implications of the use of a concept hold for any image that falls under it. The simimulational role of toys is exactly like this. The schematic coordination of the image and the concept is there, however, (1) its representational function is partially suspended, (2) the stabilized homogeneity between object and concept is frequently destabilized in favor of new modes of construction and correspondingly, object-constitution, (3) the relaxation of representational constraints amplifies constructivity so much so that we can replace a canonical set of image-models with such-and-such properties with an entirely new set that has different qualities (e.g., substituting humanoid doll-like entities with tiny calculators while abiding by the rules of how these calculators operate).

With regard to #3, simulation can be said to be essentially a species of what Kant calls as-if arguments (als ob). Such arguments are regulative judgements which can be both theoretical and practical such as as if there are categorical imperatives with regard to the kingdom of ends. In Kant’s philosophy, we should always be vigilant not to mistake a regulative judgement (an analogical as-if) for a constitutive judgement. In other words, we can never overextend our analogies. But in contrast to Kantian as-if arguments which are purely analogical and thus under the constraints of analogy, the simulational as-ifs are not exactly analogical meaning that they do not need to be always compared with or a priori limited by constitutive judgements. Simply put, we can take an analogy—a simulation to be more precise—seriously, treating it completely in its own terms. There is no danger of overextending an analogy in a simulated world so long as we are consist in our treatment of the simulated components and are true to the simulation and its logic (e.g., . Within a toy universe—i.e. a simulated framework—the primary emphasis should in fact be given to the simulation and not how the simulated is related to the source or premise of analogy). If we are to enrich a simulated world we ought to, first and foremost, attend to the simulated framework rather rather than the source of the analogy i.e. the real world. Only the unreserved enrichment of the former can assure the enrichment of our conception of the latter.

With this rather hasty discussion, let us in a crude manner define toys:

3. The Philosopher King of All Toys and Engineers

The idea of toy as an object-model capable of simulating a world or a problem without strictly conforming to the representational constraints of that world or variables and parameters of the original problem has a long history in science and specifically engineering. Confronted with a problem in one domain, the engineer constructs a toy surrogate or mechanical analog of that problem in another domain. The engineer then goes on to investigate this toy construct and how it behaves in its specific domain and in its own terms. Using certain equivalence principles that can coordinate the original problem and the toy surrogate, the engineer is then able to use the solution provided by the machine and translate it into a solution for the original problem.

It is as if in order to adequately understand a problem in a specific domain and to arrive at a solution to it, one must first attempt to exteriorize this attempt at understanding by reinventing the problem in an entirely new domain. But what would be the characteristics of this new domain? First, this new domain should allow us to examine the original problem under new parameters which are not exactly the parameters of its native domain. Next, the new domain should be far more manipulable than the old one. The principle behind this genius epistemic hack is attributed to the greatest of all engineers, Archimedes of Syracuse. It is well-known that Archimedes had a recipe to crack the most difficult geometrical problems of his time through a method of mechanical reasoning: inventing a toy machine and observe how the machine deals with your problem.

Imagine there is a geometrical problem which cannot be solved given the resources you have—or at least, it will be very difficult. Also imagine you are a cunning devil-engineer who doesn’t simply give up. You instead construct a mechanical device that can stand as the analog of your geometrical problem. The construction of such a machine would require particular and general forms of equivalence-establishment between the geometrical problem and the machine (the mechanical domain). The particular equivalence criteria consist of a set of geometrical inferences which can translate and transpose your geometrical problem into the construction and the behavior of the machine, plus an available mechanical or physical principle which can coordinate the parameters of the machine with those of the geometrical problem. The general criterion of equivalence, on the other hand, is usually a combination of simplification and/or idealization, in the sense that the machine—its scope, assignment, behavior—should be sufficiently idealized/simplified for it to be an optimal analogue of the problem at hand.

Once you make the mechanical analog, you want to pay attention to how the machine works and not the geometrical problem. When you have something similar to an output or the machine-solution, then you again use the particular criteria of equivalence so as to translate the solution supplied by the machine into a solution to your original geometrical problem. See the following diagram for a better grasp of this method (Note: the ASCII diagram might display incorrectly if you are using a feed-reader.)

            ┌──────────┐                   ┌──────────┐
            │Solution G│◁───Equivalence────│Solution M│
            └─────△────┘                   └─────△────┘
                  │                              │
                  │             .────────────────┴────────────────────.
                  │            ( bracketing the space of n-hypothesis  )
                  │             `────────────────┬────────────────────'
                  │                              │
    Geometrical  ┌┘                              └┐  Mechanical
      Reasoning┌─┘                                └─┐Reasoning
             ┌─┘            ┌──────────┐            └─┐
  ┌──────────┴──────────┐   │Mechanical│   ┌──────────┴──────────┐
  │                     ◁───┤Principle ├───┤                     │
  │ Geometrical Problem │   └──────────┘   │ Mechanical Problem  │
  │                     ├──────────────────▷                     │
  └─────────────────────┘    Geometrical   └─────────────────────┘
             │                Reasoning               │
             │                                        │
             └────────────────────┬───────────────────┘
                                  │
          .───────────────────────▽───────────────────────.
         (   Equivalence via Simplification⊕Idealization   )
          `───────────────────────────────────────────────'

For example, imagine the problem of’how much bigger is a cylinder than a sphere fully enclosed in it?’ To answer this question, we can use a lever with adjustable arms and a solid sphere and cylinder made of the same uniform material. All we need to do is to put the sphere and the cylinder on the extremes of the lever and adjust it so the two are balanced. The answer if you are willing to do this experiment is V_cyl : V_sph = 3 : 2.

A more contemporary and intricate example would be one suggested by David Hilbert in Geometry and the Imagination (p. 222). This is the problem of finding geodesics of a surface. To construct a mechanical analog, we need to have Gauss-Hertz principle of least constraint—or more precisely, Hertz principle of least curvature—as the particular criterion of the equivalence between the mechanical and the geometrical. This is our first problem before going on to build a mechanical or toy surrogate: finding the equivalence (not equality) relations.

As soon as we have the equivalence relation—Hertz principle—we can talk about and examine the constrained dynamics problem as if it was the problem of finding geodesics of a surface. The Hertz principle gives us a way of coordinating geodesics equations and equations of motion. Thus when we arrive at a solution to the constrained dynamics problem we can can translate it into a solution for finding geodesics of a surface.

In order to understand how the analog of the problem of finding geodesics of a surface works, first we begin with differential equations for a 3-dimensional surface parametrized as follows: . These differential equations can be expressed in a compact form as:

where and are Christoffel symbols.

Now, for constructing the mechanical analog of this problem, we can imagine a toy universe consisting of only two blocks, a toy-apple and a toy-ant. They are toyish because it does not matter whether the apple is red or green, or whether the ant is silicon-based or carbon-based. All we are interested in are those features which allow us to observe the locomotion-behavior of the ant as it it traverses the surface of the apple. In fact the walk of the toy-ant on the surface of the toy-apple represents a difficult problem of robotics: How can the robot-ant find the shortest paths on a generalized surface, whether on the surface of Mars or on a Riemann surface?

The apple-walking of the ant represents (holonomically constrained, i.e. ) force-free geodesics on a constrained motion surface which conforms to the following equation after constraint stabilization:

where is a constraint Jacobian matrix .

The toy apple-walking ant equation is not restricted to , it can be equally applied to . For a detailed mathematical take on how the equations of this toy universe can exactly solve the problem of finding geodesics of a surface, you can look at Least action principles and their application to constrained and task-level problems in robotics and biomechanics by De Sapio and others.

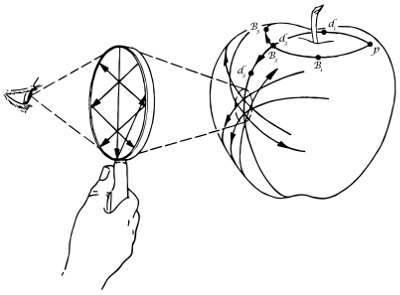
Source: Misner, Thorne, Wheeler, Gravitation (Princeton University Press).

Despite its peculiar artistry, the Archimedean method or hack is quite simple actually. But the scope of this method should not be restricted to the world of geometrical and mechanical problems. It an be applied to any problem after finding a particular equivalence relation that translates the constraints of the domain X (the milieu of the original problem) to the constraints and parameters of another domain. The legend of Archimedes in the tub captures the power of toy analogues quite spectacularly: Archimedes is in the tub, playing with water like a child, making waves after waves, watching how the water spills out of the tub. Then suddenly he pretends that his body is a gourd of water and then he continues with this experiment as if it was reality. In any case, we can think of the Archimedean method as a generalized way of playing with toys qua object-models. The following diagram should shed some light on the general logic of the Archimedean method:

                              X──────────────────────T
                              │ How-possibly-enough  │
           ┌─────────────────▷│     explanation      │◁──────────────────┐
  X────────┴────────┐         │                      │          T────────┴────────┐
  │  How-actually   │         └──────────────────────┘          │  How-possibly   │
  │  understanding  │                                           │   explanation   │
  └────────┬────────┘                                           └────────┬────────┘
           │                                                             │
           │  ┌─────────────────────┐           ┌─────────────────────┐  │
           │  │                     │           │  Toy surrogate (T)  │  │
           └──│      Problem X      │           │        of X         │──┘
              │                     │           │                     │
              └─────────────────────┘     Λ     └─────────────────────┘
                         │               ╱ ╲               │
                         │              ╱   ╲              │
                         └────────────▷▕Eq. ?▏◁────────────┘
                                        ╲   ╱
                                         ╲ ╱
                                          V

So on one side, we have the problem X. Our aim is to understand how actually this problem can be brought into a resolution. On the other side, which is that of the toy surrogate, we are free from such a mode of understanding and explanation which we can be called how-actually. We are interested in the possibilities of how the analog or the toy surrogate can explain the problem X. In a nutshell, the toy analog is both the domain of possibilities which where absent in X and the domain of bracketing or winnowing through such possibilities (the space of n-hypothesis). This is what for now can be dubbed the domain of how-possibly explanation. I will define how-actually and how-possibily explanations and their corresponding modes of understanding when I discuss toy models, but until then let us go along with these rudimentary definitions.

Once we solve the problem of establishing equivalence relations (Eq. ?), we can enter the domain of the toy analog, examine and observe how the reinvented problem comes to a resolution. Essentially, in the analog domain, the solution is not analytic in any sense. The solution can only be achieved through bracketing or limiting the space of possible hypotheses and their corresponding explanations. And that’s exactly what the Archimedean method does: it enables the how-possibly explanation brought about in the analog domain to become a how-actually understanding for the original problem in the domain X. For once we arrive at a true enough how-possibly explanation in the toy domain—namely, a candidate hypothesis and its corresponding explanation—we can say that this is also a how-actually enough (i.e. true) explanation or resolution for the problem in the domain X.

This post has gone beyond the limits I originally imagined, so let’s stop at this point and wait for the next installment in this series. [Update note: For those of you who are interested, I have added some equations for the Hertz-principle example mentioned in the last section.]